Hidden Markov Model im Video: Hintergründe zum iPhone 5s Bewegungstracker

Inzwischen haben wir den neuen Coprozessor des iPhone 5s, den Logik-Baustein M7, ganz gut kennen gelernt. Wir wissen, dass sich der Chip – fast ohne zusätzlichen Stromverbrauch – um die durchgängige Analyse der vom iPhone wahrgenommenen Bewegungen kümmert und diese aufzeichnet.

Wir kennen die Applikationen, die die Bewegungsdaten anzeigen können und euch so bei der Überwachung der zurückgelegten Schritte helfen. Wir wissen, dass sich das iPhone 5s die Bewegungsmuster der vergangenen sieben Tage merkt, zwischen unterschiedlichen Aktivitäten (laufen, sitzen, motorisierte Fortbewegung) unterscheiden kann und den Entwicklern, die mit den Daten arbeiten, auch darüber informiert, wie treffsicher Ansagen wie „zwischen 14:30 Uhr und 15:12 Uhr ist der Nutzer gejoggt“ voraussichtlich sind. Ihr erinnert euch an das Bayes-Theorem.

Doch welche mathematischen Aspekte müssen iPhone-Entwickler bei der Arbeit mit dem M7-Prozessor berücksichtigen?

Paul Balzer, Algorithmus-Experte bei Mechlab Engineering, stellt in dem unten eingebetteten Video das Hidden Markov Model vor, mit dem sich die Wahrscheinlichkeit von Nutzer-Aktivitäten ermitteln lässt. Der 8 Minuten Clip erklärt Übergangswahrscheinlichkeiten und beschreibt welche Daten berücksichtigt werden müssen, um zutreffende Aussagen über den gerade vorliegenden Aktivitäts-Typ treffen zu können.

Sehr verkopft und gleichzeitig sehr interessant:

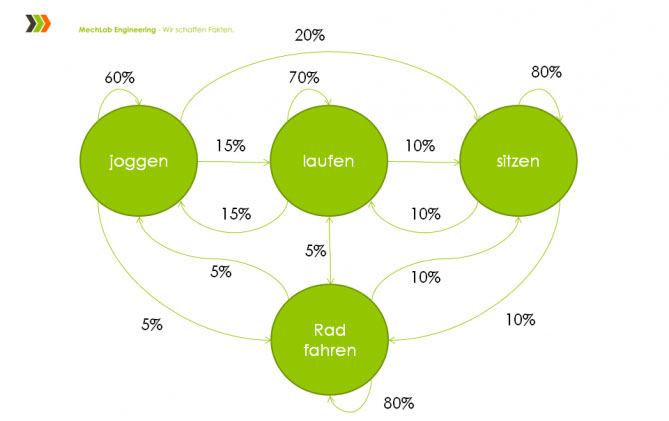
Allein mit Hilfe der Drehrate und Beschleunigung ist es relativ einfach möglich, grundlegende Aktivitäten zu unterscheiden. Der hier aufgezeichnete und betrachtete Zeitraum war nur 8 Sekunden. Mit den Ergebnissen aus jeweils einer Periode kann eine Wahrscheinlichkeit berechnet werden, welche Aktivität gerade vorliegt. Z.B. könnte aus der Analyse der Signale berechnet werden, dass gerade Fahrrad gefahren wird.

Kommt der Algorithmus zu dem Ergebnis “radfahren”, so wird die Wahrscheinlichkeit, dass gerade wirklich Rad gefahren wird, erhöht. So kann über das Bayes’-Theorem mit vorhandener Wahrscheinlichkeit und neuer Erkenntnis eine “confidence” berechnet und ausgegeben werden. Zusätzlich können Zustandsübergänge als Markoff Ketten mit Wahrscheinlichkeiten bestimmt werden. Ein Übergang von joggen zu laufen ist wahrscheinlicher, als ein Übergang von joggen zu radfahren.